Potęgowanie
Potęga to uogólniony zapis wielokrotnego mnożenia elementu przez siebie. Zapis xⁿ oznacza n-krotne mnożenie przez siebie x.
xⁿ = x • x • x • … • x, gdzie n = ilość x
Potęgowany element (n) nazywamy podstawą, a liczba mnożeń, zapisywana u góry (w tzw. indeksie górnym) to wykładnik potęgi.
Przykład: 4³ = 4 • 4 • 4 = 64
x° = 1 gdy x ≠ 0
Przykład: 8° = 1
X¹ = X
Przykład: 2¹ = 2
Druga potęga to kwadrat danej liczby (x²), trzecia to sześcian (x³).
-

Przykład:
-
 gdy x ≠ 0
gdy x ≠ 0
Przykład:
-

Przykład:
- (x + y)ⁿ = xⁿ • yⁿ
Przykład: (6 • 2)² = 6² • 2² = 36 • 4 = 144
-
 jeśli y ≠ 0
jeśli y ≠ 0
Przykład:
-
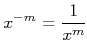 gdy x ≠ 0
gdy x ≠ 0
Przykład: .
.
Pierwiastkowanie
Pierwiastkowanie to działanie odwrotne do potęgowania. Symbolem pierwiastka jest ![]() .Pierwiastkiem stopnia n liczby a jest liczba b. Zapisujemy to w ten sposób:
.Pierwiastkiem stopnia n liczby a jest liczba b. Zapisujemy to w ten sposób:
![]()
a – liczba podpierwiastkowa
n – stopień pierwiastka (jeśli pierwiastek jest kwadratowy to pole jest puste)
b – pierwiastek n-tego stopnia z a (czyli wynik pierwiastkowania)
- Pierwiastkiem liczby 1 jest liczba 1, bo 1 • 1 = 1
- Pierwiastkiem liczby 4 jest liczba 2, bo 2 • 2 = 4
- Pierwiastkiem liczby 9 jest liczba 3, bo 3 • 3 = 9
- Pierwiastkiem liczby 16 jest liczba 4, bo 4 • 4 = 16
- Pierwiastkiem liczby 25 jest liczba 5, bo 5 • 5 = 25
- Pierwiastkiem liczby 36 jest liczba 6, bo 6 • 6= 36 ...itd.
Zapisujemy to w ten sposób:
![]() = 1, bo 12 = 1
= 1, bo 12 = 1![]() = 2, bo 22 = 4
= 2, bo 22 = 4![]() = 3, bo 32 = 9
= 3, bo 32 = 9![]() = 4, bo 42 = 16
= 4, bo 42 = 16![]() = 5, bo 52 = 25
= 5, bo 52 = 25![]() = 6, bo 62 = 36 ...itd.
= 6, bo 62 = 36 ...itd.
Pamiętajmy, że ![]() , ponieważ 00 to symbol nieoznaczony.
, ponieważ 00 to symbol nieoznaczony.

Własności (prawa działań na pierwiastkach)
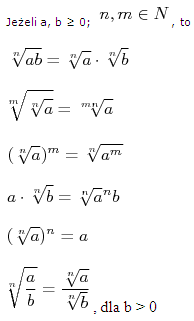
Pierwiastek stopnia drugiego (n = 2) to pierwiastek kwadratowy. Pierwiastek stopnia trzeciego (n = 3) to pierwiastek sześcienny. Zapisujemy go tak: ![]() . Pierwiastek czwartego stopnia (n = 4) zapisujemy:
. Pierwiastek czwartego stopnia (n = 4) zapisujemy: ![]() .
.





