Przed Tobą test maturalny, składający się z 34 zadań. Maksymalna ilość punktów do uzyskania to 50. Aby zaliczyć test, należy uzyskać minimum 30%, a więc 15 punktów. Rozwiąż zadania, a potem sprawdź wyniki z odpowiedziami na dole strony.
Test maturalny 1
|
Nr pytania |
Zadanie |
Odpowiedzi |
Liczba punktów |
|
1 |
Rozwiąż układ równań: 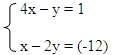
|
a) x = 3, y = 6 b) x = 4, y = -3 c) x = 2, y = 7 d) x = y |
2 |
|
2 |
Napisz równanie okręgu stycznego do OX o środku w punkcie S(-7, 2). |
a) (x-7)² + (y +2)² = 49 b) (x+7)² + (y -2)² = 49 c) (x-2)² + (y +7)² = 49 d) (x+2)² + (y -7)² = 49 |
2 |
|
3 |
Przeciwlegle wierzchołki prostokąta B i D mają współrzędne: B(2, -4) i D(-2, 4). Oblicz długość przekątnej tego prostokąta. |
a) 3√5 b) 2√3 c) 5√2 d) 2√5 |
2 |
|
4 |
Rozwiąż równanie: x² - 4x + 2 = 0 |
a)x=√2 lub x= -√2 b)x = 2-√2 lub x= 2+√2 c)x= -2 lub x=2 d)x=2-√8 lub x=2+√8 |
2 |
|
5 |
Liczby: 3,9,x+4 są pierwszym, trzecim i siódmym wyrazem ciągu arytmetycznego. Oblicz x. |
a) x=17 b) x=3 c) x=23 d) x=11 |
2 |
|
6 |
Rzucamy dwoma kostkami i za każdym razem sumujemy oczka wyrzucone na obu kostkach. Jakie jest prawdopodobieństwo wyrzucenie sumy 7? |
a) 1/36 b) 7/36 c) 1/6 d) 5/18 |
2 |
|
7 |
Przekątna ściany bocznej sześcianu ma długość √3. Oblicz długość przekątnej sześcianu. |
a) 4 b)2 c)2√3 d) √3 |
2 |
|
8 |
Wskaż miejsca zerowe dla : 
|
a) -2/3, ¼ b) -1/4, 2/3 c) ½, ¾ d) -1/2, -2/3 |
2 |
|
9 |
Jakie jest prawdopodobieństwo wylosowania liczby podzielnej przez 5 ze zbioru dwucyfrowych liczb naturalnych? |
a) 1/100 b) 15/90 c) 19/86 d) 17/91 |
2 |
|
10 |
Narysuj wykres funkcji f(x) = (x+2)2- 4 |
2 |
|
|
11 |
Pierwszego dnia na zajęcia koła matematycznego przeszło 36 osób z klasy I i maturalnej. Za tydzień liczba uczniów klasy maturalnej potroiła się a uczniów z klasy I było o 2 mniej. Ogólna liczba uczestników zajęć podwoiła się. Ilu uczniów z klasy I a ilu z maturalnej przyszło pierwszego dnia na zajęcia? |
a) I – 17, III – 19 b) I – 15, III – 21 c) I – 30, III - 13 d) I – 24, III - 24 |
3 |
|
12 |
|
 |
1 |
|
13 |
Wskaż ilość miejsc zerowych funkcji: 7x² + 3x + 2 = 0 |
a) 2 b) 1 c) 0 d) 3 |
1 |
|
14 |
Zbiorem wartości funkcji 7x² + 3x + 2 = 0 jest: |
a) y > 0 b) y < 0 c) y = 0 d) y ≠ 0 |
1 |
|
15 |
|
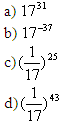 |
1 |
|
16 |
2log 5 + log 3 = |
a) log30 b) log15 c) log17 d)2log8 |
1 |
|
17 |
Funkcja f(x) = (m – 5)x² + 2x – 1, przechodzi przez punkt (1, 18). Oblicz m. |
a)17 b) 3 c) 22 d) 18 |
1 |
|
18 |
Do wykresu funkcji f(x) = 3x² + 3 należy punkt: |
a) (7, 3) b) (-8, -2) c) (1, 6) d) (-1, -6) |
1 |
|
19 |
Zbiorem rozwiązań nierówności: |2x – 4| ≤ 2 jest: |
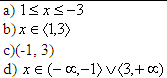 |
1 |
|
20 |
Która z funkcji jest równoległa do y = 3x – 4? |
a) y = 3x – 5 b) y = -3x -4 c) y = 1/3x +4 d) y = - 1/3x -4 |
1 |
|
21 |
Która z funkcji jest prostopadła do y = 1/4x +2? |
a) y =-1/4x+2 b) y = -4x +2 c) y = 4x+2 d) y = 1/4x +3 |
1 |
|
22 |
|
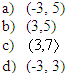 |
1 |
|
23 |
Ile rozwiązań rzeczywistych ma równanie: 17x² - 25 = 0? |
a) 0 b) 2 c) 3 d) 4 |
1 |
|
24 |
Podany zbiór |
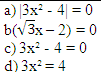 |
1 |
|
25 |
Nierówność 3x² - 2 ≥ 0 ma rozwiązanie: |
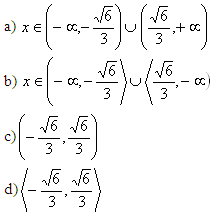 |
1 |
|
26 |
Jeśli liczba 36 stanowi 15% liczby x, to: |
a) x = 612 b) x = 2,4 c) x = 240 d) x = 0,42 |
1 |
|
27 |
Liczba 5 jest rozwiązaniem równania: |
 |
1 |
|
28 |
Liczba z stanowi 210% liczby y, zatem: |
a) z = 210y b) z = y + 210% c) z = 2y + 10%y d) y = z + 210% |
1 |
|
29 |
Dziedziną równania 3x² - 2x +1 = 0 jest: |
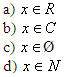 |
1 |
|
30 |
Jeżeli pierwiastkami równania jest zbiór |
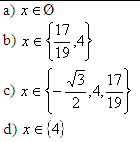 |
1 |
|
31 |
|
a) y = -(x + 2)² = 3 b) y = (x + 2)² - 3 c) y = x² - 2 d) y = (x – 3)² - 3
|
1 |
|
32 |
Wskaż ilość rozwiązań równania |
a) 0 b) 2 c) 1 d) 3 |
1 |
|
33 |
Napisz równania asymptot dla równania |
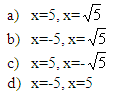 |
1 |
|
34 |
Dany jest trójkąt ABC taki jak na rysunku:  Oblicz pole tego trójkąta. |
a) P = 26, 25 b) P = 24 c) P = 15 d) P = 6√3 |
5 |
Rozwiązania
Zad. 1: C, zad. 2: B, zad. 3: D, zad. 4: B, zad. 5: A, zad. 6: C, zad. 7: B, zad. 8: C, zad. 9: D, zad. 10: A (rysunek poniżej), zad. 11: A, zad. 12: A, zad. 13: C, zad. 14: A, zad. 15: B, zad. 16: A, zad. 17: C, zad. 18: C, zad. 19: B, zad. 20: A, zad. 21: B, zad. 22: B, zad. 23: B, zad. 24: B, zad. 25: A, zad. 26: C, zad. 27: D, zad. 28: C, zad. 29: C, zad. 30: D, zad. 31: A, zad. 32: C, zad. 33: D, zad. 34: A.
Do zadania 10:
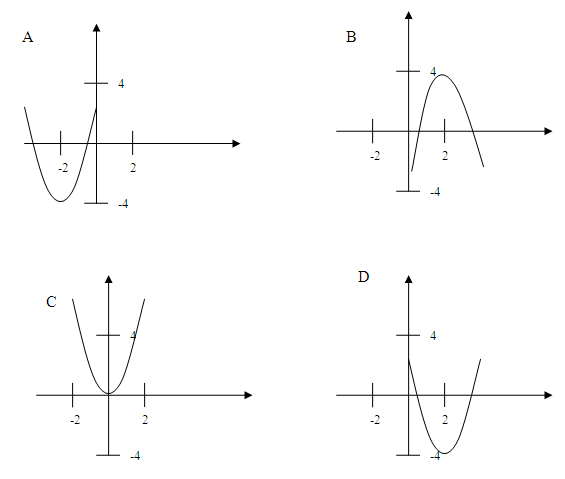


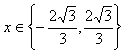 nie jest rozwiązaniem równania:
nie jest rozwiązaniem równania: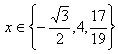 , a dziedziną równania jest zbiór liczb N, to wynika stąd, że rozwiązaniem równania jest:
, a dziedziną równania jest zbiór liczb N, to wynika stąd, że rozwiązaniem równania jest:


