Funkcją określoną na zbiorze X o wartościach w zbiorze Y nazywamy tylko takie przyporządkowanie (odwzorowanie), w którym każdemu elementowi zbioru X zostaje przyporządkowany dokładnie jeden element zbioru Y. Funkcję tę oznaczamy f:X –> Y.
Zwyczajowo funkcję oznacza się małymi literami, np. f, g, h.
Jeżeli zbiory X i Y są niepustymi podzbiorami zbioru liczb rzeczywistych (
, 
), to funkcję 
nazywamy funkcją liczbową zmiennej rzeczywistej.
Dziedzina i zbiór wartości funkcji
Dziedzina jest to zbiór wszystkich argumentów danej funkcji.
Zbiór X nazywamy dziedziną funkcji a zbiór Y przeciwdziedziną funkcji.
Zbiorem wartości funkcji f nazywamy zbiór wartości należących do zbioru Y, któremu zostały przyporządkowane elementy ze zbioru X.
Zbiór wartości funkcji f (oznaczany symbolem 
) to zbiór wszystkich elementów postaci f(x) dla 
.
Zapis „f (x) = 4” czytamy: dla argumentu x funkcja f przyjmuje wartość 4.
Sposoby przedstawiania funkcji
Funkcję można przedstawić na parę sposobów:
- przepisem słownym,
- tabelką,
- grafem,
- jako zbiór par uporządkowanych,
- wzorem,
- wykresem (graficznie).
JAK PRZEDSTAWIĆ FUNKCJĘ ZA POMOCĄ:
• Przepisu słownego:
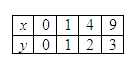
„Dane są zbiory X = {0, 1, 4, 9}, Y = {0, 1, 2, 3}, wówczas każdej liczbie ze zbioru X przyporządkowujemy jej pierwiastek kwadratowy”.
• Tabelki:
• Grafu:
x y
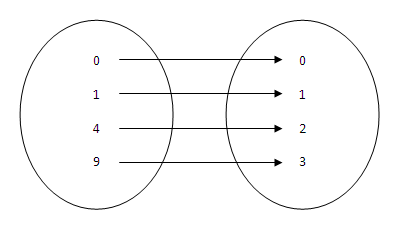
f: X –> Y
• Zbioru par uporządkowanych:
{ (0, 0), (1, 1), (4, 2), (9, 3) }
• Wzoru:
, gdzie 
lub
, gdzie 
lub
, gdzie 
• Wykresu:
Wykresem funkcji liczbowej nazywamy zbiór tych wszystkich punktów płaszczyzny o współrzędnych (x, y), w prostokątnym układzie współrzędnych, gdzie x jest argumentem funkcji, y zaś wartością funkcji dla argumentu x.
Funkcja liniowa
Funkcją liniową nazywamy funkcję określoną wzorem f(x) = ax + b, gdzie a, b są dowolnymi stałymi rzeczywistymi.
Miejsce zerowe
Miejscem zerowym funkcji y = f(x) nazywamy liczbę x1, która spełnia warunek f(x1) = 0.
Jeżeli 
, to funkcja liniowa jest funkcją różnowartościową i posiada jedno miejsce zerowe (x, 0), gdzie 
. Interpretacja graficzna miejsca zerowego to punkt, w którym wykres funkcji przecina bądź styka się z osią OX w układzie współrzędnych.
Jeśli funkcja nie jest funkcją stałą, posiada dokładnie jedno miejsce zerowe.
Jeśli funkcja jest funkcją stałą, to albo nie posiada miejsc zerowych (b ≠ 0), albo wszystkie jej argumenty są miejscami zerowymi (b = 0).
- a > 0 – funkcja rosnąca
- a < 0 – funkcja malejąca
- a = 0 – funkcja stała
Tę właściwość nazywamy monotonicznością funkcji liniowej.
funkcja rosnąca funkcja malejąca funkcja stała
Równość funkcji
Funkcje f i g są równe wtedy i tylko wtedy, gdy mają identyczne dziedziny oraz dla każdego argumentu należącego do ich wspólnej dziedziny wartości obu funkcji są jednakowe.
Definicja (iloczyn liczby przez funkcję):
Jeśli 
, a f jest funkcją liczbową, to kf jest funkcją określoną następująco: 
, gdzie 
.
