Kombinatoryka to teoria obliczania liczby elementów zbiorów skończonych. Jest jednym z działów matematyki dyskretnej, a powstała dzięki rachunkowi prawdopodobieństwa i obserwacjom gier liczbowych w XVII w.
Teoria prawdopodobieństwa
Teoria prawdopodobieństwa, inaczej rachunek prawdopodobieństwa lub probabilistyka, to dział matematyki zajmujący się zdarzeniami losowymi. Teoria prawdopodobieństwa jest fundamentalna dla statystyki.
Prawdopodobieństwem zdarzenia A nazywamy iloraz liczby zdarzeń elementarnych sprzyjających zdarzeniu A i liczby wszystkich zdarzeń elementarnych.
Doświadczeniem losowym nazywamy doświadczenie, które można powtarzać wielokrotnie w jednakowych lub zbliżonych warunkach i którego wyniku nie można przewidzieć (np. rzut monetą lub kostką do gry).
Zdarzenie elementarne to najprostszy wynik doświadczenia losowego.
Zdarzenie losowe to dowolny podzbiór skończonego zbioru zdarzeń elementarnych.
A – zdarzenie losowe
|A| – liczba zdarzeń elementarnych w A
Ω – zbiór wszystkich możliwych zdarzeń elementarnych
|Ω| – liczba zdarzeń elementarnych w Ω
Prawdopodobieństwo zajścia zdarzenia A: 
Silnia
n – liczba naturalna
n! – n silnia
Silnia z liczby naturalnej n jest oznaczana przez n!. Dla n = 0 lub n = 1 wynosi ona 1, natomiast dla n ≥ 2 jest równa iloczynowi wszystkich liczb naturalnych od 1 do n.

Permutacje
Ciąg utworzony z wszystkich n elementów zbioru nazywamy jego permutacją. Liczbę wszystkich permutacji danego n-elementowego zbioru obliczamy wg wzoru ![]() .
.
Wariacje
• Wariacją z powtórzeniami nazywamy ciąg o długości k, którego wyrazy pochodzą z n-elementowego zbioru. Liczbę wszystkich wariacji danego zbioru obliczamy ze wzoru ![]() .
.
• Wariacją bez powtórzeń nazywamy ciąg k wyrazów, nie powtarzających się, które są elementami danego zbioru o liczności n. Ilość wszystkich wariacji obliczamy ze wzoru  .
.
Kombinacje
Kombinacja k-elementowa ze zbioru n-elementowego nazywamy dowolny podzbiór k-elementowy danego zbioru n-elementowego. W podzbiorach kolejnosc elementów nie jest wazna.
Dwumian Newtona
Dwumian Newtona to wzór, za pomocą którego możemy obliczyć potęgi sumy dwóch liczb.
Wzór na dwumian Newtona:
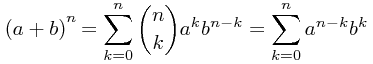
Symbol Newtona
Liczba  dla
dla ![]() , gdzie
, gdzie ![]() .
.
Symbol Newtona ![]() czytamy „n po k”.
czytamy „n po k”.
Symbol Newtona jest zawsze liczbą naturalną.